24 Confirmatory factor analysis
Confirmatory factor analysis or CFA is used to confirm an appropriate factor structure for an instrument. Whereas EFA provides tools for exploring factor structure, it does not allow us to modify specific features of our model beyond the number of factors. Furthermore, EFA does not formally support the testing of model fit or statistical significance in our results. CFA extends EFA by providing a framework for proposing a specific measurement model, fitting the model, and then testing statistically for the appropriateness or accuracy of the model given our instrument and data.
Note that CFA falls within a much broader and more general class of structural equation modeling (SEM) methods. Other applications of SEM include path analysis, multilevel regression modeling, and latent growth modeling. CFA and SEM models can be fit and analyzed in R, but, given their complexity, commercial software is often preferable, depending on the model and type of data used. For demonstration purposes, we will examine CFA in R using the lavaan package.
The BDI-II
Let’s consider again the BDI-II, discussed above in terms of EFA. Exploring the factor structure of the instrument gives us insights into the number of factors needed to adequately capture certain percentages of the variability in scores. Again, results indicate that two factors, labeled in previous studies as cognitive and somatic, account for about a quarter of the total score variance. In the plot above, these two factors clearly stand out above the scree. But the question remains, is a two factor model correct? And, if so, what is the best configuration of item loadings on those two factors?
In the end, there is no way to determine with certainty that a model is correct for a given data set and instrument. Instead, in CFA a model can be considered adequate or appropriate based on two general criteria. The first has to do with the explanatory power of the model. We might consider a model adequate when it exceeds some threshold for percentage of variability explained, and thereby minimizes in some way error variance or variability unexplained. The second criterion involves the relative appropriateness of a given model compared to other competing models. Comparisons are typically made using statistical estimates of model fit, as discussed below.
Numerous studies have employed CFA to test for the appropriateness of a two factor structure in the BDI-II. Whisman, Perez, and Ramel (2000) proposed an initial factor structure that included five BDI-II items loading on the somatic factor, and 14 items loading on the cognitive factor (the authors label this factor cognitive-affective). The remaining two items, Pessimism and Loss of Interest in Sex, had been found in exploratory analyses not to load strongly on either factor. Thus, loadings for these were not estimated in the initial CFA model.
Results for this first CFA showed poor fit. Whisman, Perez, and Ramel (2000) reported a few different fit indices, including a Comparative Fit Index (CFI) of 0.80 and a Root Mean Square Error of Approximation (RMSEA) of 0.08. Commonly used thresholds for determining “good fit” are CFI at or above 0.90 and RMSEA at or below 0.05.
An important feature of factor analysis that we have not yet discussed has to do with the relationships among item errors. In EFA, we assume that all item errors are uncorrelated. This means that the unexplained variability for a given item does not relate to the unexplained variability for any other. Similar to the CTT model, variability in EFA can only come from the estimated factors or random, uncorrelated noise. In CFA, we can relax this assumption by allowing certain error terms to correlate.
Whisman, Perez, and Ramel (2000) allowed error terms to correlate for the following pairs of items: sadness and crying, self-dislike and self-criticalness, and loss of pleasure and loss of interest. This choice to have correlated errors seems justified, given the apparent similarities in content for these items. The two factors in the initial CFA didn’t account for the fact that respondents would answer similarly within these pairs of items. Thus, the model was missing an important feature of the data.
Having allowed for correlated error terms, the two unassigned items Pessimism and Loss of Interest in Sex were also specified to load on the cognitive factor. The result was a final model with more acceptable fit statistics, including CFI of 0.90 and RMSEA of 0.06.
24.1 Steps in CFA
Here, we will fit the final model from Whisman, Perez, and Ramel (2000), while demonstrating the following basic steps in conducting a CFA:
- hypothesizing the proposed factor structure with necessary constraints,
- preparing our data and fitting the CFA model,
- evaluating the model and statistically testing for model fit,
- revising the model, comparing to more or less complex models, and repeating evaluation and testing of fit as needed.
1. Hypothesize the factor structure
As discussed previously, we hypothesize that two factors will be sufficient for explaining the correlations among items in the BDI-II. These factors are labeled cognitive and somatic, based on the content of the items that tend to load on them. We also hypothesize that the two factors will be correlated. Finally, we allow for correlated errors between sadness and crying, self-dislike and self-criticalness, and loss of pleasure and loss of interest.
Figure 24.1 is a visual representation of the CFA model we’re fitting. On the left are the two factors, and on the right are the observed item variables. Estimates for the correlation between factors, the factor loadings, and item variances are also shown.
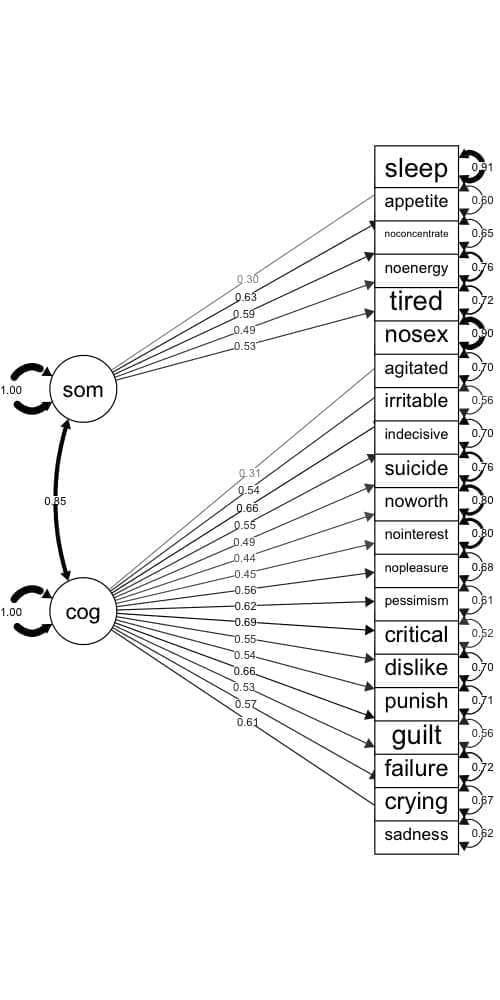
Figure 24.1: CFA model for the BDI-II, with factor loadings and error variances.
2. Prepare the data, fit the model
We assume that the scored item responses on the BDI-II represent continuous variables. The covariance matrix in BDI$S was obtained using the 576 respondents having complete data across all 21 items. As reported in Whisman, Perez, and Ramel (2000), the mean total score was 8.36 with SD 7.16. Thus, on average, respondents were in the minimal depression score range, though some had scores in the mild and moderate ranges, and a few fell in the severe range.
Considering the complexity of our model, the sample size of 576 should be sufficient for estimation purposes. Since different CFA models can involve different numbers of estimated parameters for the same number of items, sample size guidelines are usually stated in terms of the number of parameters rather than the number of items. We’ll consider the recommended minimum of five times as many people as parameters. The total number of parameters estimated by our model will be 43, with 21 factor loadings, 21 error variances, and the correlation between the cognitive and somatic factors.
We fit our CFA using the covariance matrix in BDI$S. The cfa() function in the lavaan package requires that we name each factor and then list out the items that load on it after the symbol =~. Here, we label our cognitive factor cog and somatic factor som. The items listed after each factor must match the row or column names in the covariance matrix, and must be separated by +.
The lavaanify() function will automatically add error variances for each item, and the correlation between factors, so we don’t have to write those out. We do need to add the three correlated error terms, for example, with sadness ~~ crying, where the ~~ indicates that the variable on the left covaries with the one on the right.
The model is fit using the cfa() function. We supply the model specification object that we created above, along with the covariance matrix and sample size.
# CFA of BDI using the lavaan package
# Specify the factor structure
# Comments within the model statement are ignored
bdimod <- lavaanify(model = "
# Latent variable definitions
cog =~ sadness + crying + failure + guilt + punish +
dislike + critical + pessimism + nopleasure +
nointerest + noworth + suicide + indecisive +
irritable + agitated + nosex
som =~ tired + noenergy + noconcentrate + appetite +
sleep
# Covariances
sadness ~~ crying
dislike ~~ critical
nopleasure ~~ nointerest",
auto.var = TRUE, auto.cov.lv.x = TRUE, std.lv = TRUE)
# Fit the model
bdicfa <- cfa(bdimod, sample.cov = BDI$S,
sample.nobs = 576)3. Evaluate the model
To evaluate the model that’s stored in the object bdicfa, we send it to the lavaan summary() function, while requesting fit indices with the argument fit = TRUE. Lots of output are printed to the console, including a summary of the model estimation, some fit statistics, factor loadings (under Latent Variables), covariances, and variance terms (including item errors).
The CFI and RMSEA are printed in the top half of the output. Neither statistic reaches the threshold we’d hope for. CFI is 0.84 and RMSEA is 0.07, indicating less than optimal fit.
Standardized factor loadings are shown in the last column of the Latent Variables output. Some of the loadings match up well with those reported in the original study. Others are different. The discrepancies may be due to the fact that our CFA was run on correlations rounded to two decimal places that were converted using standard deviations to covariances, whereas raw data were used in the original study. Rounding can result in a loss of meaningful information.
# Print fit indices, loadings, and other output
summary(bdicfa, fit = TRUE, standardized = TRUE)
#> lavaan 0.6-9 ended normally after 41 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 46
#>
#> Number of observations 576
#>
#> Model Test User Model:
#>
#> Test statistic 737.735
#> Degrees of freedom 185
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3666.723
#> Degrees of freedom 210
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.840
#> Tucker-Lewis Index (TLI) 0.818
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -9585.792
#> Loglikelihood unrestricted model (H1) -9216.925
#>
#> Akaike (AIC) 19263.585
#> Bayesian (BIC) 19463.966
#> Sample-size adjusted Bayesian (BIC) 19317.934
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.072
#> 90 Percent confidence interval - lower 0.067
#> 90 Percent confidence interval - upper 0.078
#> P-value RMSEA <= 0.05 0.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.057
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> cog =~
#> sadness 0.349 0.022 15.515 0.000 0.349 0.613
#> crying 0.315 0.022 14.267 0.000 0.315 0.572
#> failure 0.314 0.024 13.140 0.000 0.314 0.533
#> guilt 0.391 0.023 17.222 0.000 0.391 0.663
#> punish 0.329 0.025 13.339 0.000 0.329 0.540
#> dislike 0.290 0.022 13.462 0.000 0.290 0.547
#> critical 0.472 0.026 18.233 0.000 0.472 0.695
#> pessimism 0.412 0.026 15.935 0.000 0.412 0.624
#> nopleasure 0.225 0.016 14.012 0.000 0.225 0.563
#> nointerest 0.373 0.035 10.795 0.000 0.373 0.450
#> noworth 0.261 0.025 10.637 0.000 0.261 0.443
#> suicide 0.268 0.023 11.859 0.000 0.268 0.488
#> indecisive 0.358 0.026 13.661 0.000 0.358 0.551
#> irritable 0.390 0.023 17.179 0.000 0.390 0.662
#> agitated 0.327 0.024 13.494 0.000 0.327 0.545
#> nosex 0.225 0.031 7.200 0.000 0.225 0.309
#> som =~
#> tired 0.295 0.024 12.048 0.000 0.295 0.527
#> noenergy 0.375 0.033 11.202 0.000 0.375 0.494
#> noconcentrate 0.425 0.031 13.748 0.000 0.425 0.591
#> appetite 0.391 0.026 14.825 0.000 0.391 0.630
#> sleep 0.137 0.021 6.523 0.000 0.137 0.299
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .sadness ~~
#> .crying 0.009 0.009 1.007 0.314 0.009 0.045
#> .dislike ~~
#> .critical -0.029 0.010 -2.919 0.004 -0.029 -0.133
#> .nopleasure ~~
#> .nointerest 0.039 0.011 3.572 0.000 0.039 0.158
#> cog ~~
#> som 0.847 0.028 30.370 0.000 0.847 0.847
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .sadness 0.203 0.013 15.727 0.000 0.203 0.625
#> .crying 0.203 0.013 15.948 0.000 0.203 0.672
#> .failure 0.249 0.015 16.193 0.000 0.249 0.716
#> .guilt 0.195 0.013 15.424 0.000 0.195 0.560
#> .punish 0.263 0.016 16.165 0.000 0.263 0.709
#> .dislike 0.196 0.012 16.006 0.000 0.196 0.700
#> .critical 0.239 0.016 14.991 0.000 0.239 0.517
#> .pessimism 0.265 0.017 15.715 0.000 0.265 0.610
#> .nopleasure 0.109 0.007 16.043 0.000 0.109 0.683
#> .nointerest 0.549 0.033 16.451 0.000 0.549 0.798
#> .noworth 0.279 0.017 16.492 0.000 0.279 0.804
#> .suicide 0.230 0.014 16.359 0.000 0.230 0.762
#> .indecisive 0.294 0.018 16.117 0.000 0.294 0.697
#> .irritable 0.195 0.013 15.435 0.000 0.195 0.562
#> .agitated 0.253 0.016 16.142 0.000 0.253 0.703
#> .nosex 0.481 0.029 16.764 0.000 0.481 0.905
#> .tired 0.226 0.015 15.157 0.000 0.226 0.723
#> .noenergy 0.436 0.028 15.458 0.000 0.436 0.756
#> .noconcentrate 0.337 0.023 14.387 0.000 0.337 0.651
#> .appetite 0.231 0.017 13.737 0.000 0.231 0.603
#> .sleep 0.192 0.012 16.521 0.000 0.192 0.911
#> cog 1.000 1.000 1.000
#> som 1.000 1.000 1.0004. Revise as needed
The discouraging CFA results may inspire us to modify our factor structure in hopes of improving model fit. Potential changes include the removal of items with low factor loadings, the correlating of more or fewer error terms, and the evaluation of different numbers of factors. Having fit multiple CFA models, we can then compare fit indices and look for relative improvements in fit for one model over another.
Let’s quickly examine a CFA where all items load on a single factor. We no longer have correlated error terms, and item errors are again added automatically. We only specify the loading of all items on our single factor, labeled depression.
# Specify the factor structure
# Comments within the model statement are ignored as
# comments
bdimod2 <- lavaanify(model = "
depression =~ sadness + crying + failure + guilt +
punish + dislike + critical + pessimism + nopleasure +
nointerest + noworth + suicide + indecisive +
irritable + agitated + nosex + tired + noenergy +
noconcentrate + appetite + sleep",
auto.var = TRUE, std.lv = TRUE)
# Fit the model
bdicfa2 <- cfa(bdimod2, sample.cov = BDI$S,
sample.nobs = 576)
# Print output
summary(bdicfa2, fit = TRUE, standardized = TRUE)
#> lavaan 0.6-9 ended normally after 29 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 42
#>
#> Number of observations 576
#>
#> Model Test User Model:
#>
#> Test statistic 792.338
#> Degrees of freedom 189
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 3666.723
#> Degrees of freedom 210
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.825
#> Tucker-Lewis Index (TLI) 0.806
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -9613.094
#> Loglikelihood unrestricted model (H1) -9216.925
#>
#> Akaike (AIC) 19310.188
#> Bayesian (BIC) 19493.144
#> Sample-size adjusted Bayesian (BIC) 19359.811
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.074
#> 90 Percent confidence interval - lower 0.069
#> 90 Percent confidence interval - upper 0.080
#> P-value RMSEA <= 0.05 0.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.058
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> depression =~
#> sadness 0.352 0.022 15.780 0.000 0.352 0.619
#> crying 0.313 0.022 14.230 0.000 0.313 0.569
#> failure 0.305 0.024 12.736 0.000 0.305 0.518
#> guilt 0.394 0.023 17.432 0.000 0.394 0.669
#> punish 0.322 0.025 13.059 0.000 0.322 0.529
#> dislike 0.281 0.021 13.082 0.000 0.281 0.530
#> critical 0.462 0.026 17.798 0.000 0.462 0.679
#> pessimism 0.407 0.026 15.751 0.000 0.407 0.618
#> nopleasure 0.224 0.016 13.974 0.000 0.224 0.560
#> nointerest 0.381 0.034 11.106 0.000 0.381 0.460
#> noworth 0.264 0.024 10.781 0.000 0.264 0.448
#> suicide 0.270 0.023 11.999 0.000 0.270 0.492
#> indecisive 0.361 0.026 13.843 0.000 0.361 0.556
#> irritable 0.384 0.023 16.846 0.000 0.384 0.651
#> agitated 0.335 0.024 13.954 0.000 0.335 0.560
#> nosex 0.234 0.031 7.520 0.000 0.234 0.321
#> tired 0.279 0.023 12.174 0.000 0.279 0.498
#> noenergy 0.329 0.032 10.391 0.000 0.329 0.433
#> noconcentrate 0.374 0.029 12.789 0.000 0.374 0.520
#> appetite 0.331 0.025 13.192 0.000 0.331 0.534
#> sleep 0.138 0.020 7.013 0.000 0.138 0.301
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .sadness 0.200 0.013 15.800 0.000 0.200 0.617
#> .crying 0.204 0.013 16.068 0.000 0.204 0.677
#> .failure 0.254 0.016 16.279 0.000 0.254 0.732
#> .guilt 0.192 0.012 15.442 0.000 0.192 0.553
#> .punish 0.267 0.016 16.237 0.000 0.267 0.720
#> .dislike 0.202 0.012 16.234 0.000 0.202 0.719
#> .critical 0.249 0.016 15.351 0.000 0.249 0.539
#> .pessimism 0.269 0.017 15.805 0.000 0.269 0.618
#> .nopleasure 0.110 0.007 16.107 0.000 0.110 0.686
#> .nointerest 0.542 0.033 16.466 0.000 0.542 0.789
#> .noworth 0.278 0.017 16.498 0.000 0.278 0.800
#> .suicide 0.229 0.014 16.368 0.000 0.229 0.758
#> .indecisive 0.291 0.018 16.127 0.000 0.291 0.691
#> .irritable 0.200 0.013 15.579 0.000 0.200 0.576
#> .agitated 0.247 0.015 16.110 0.000 0.247 0.687
#> .nosex 0.477 0.028 16.754 0.000 0.477 0.897
#> .tired 0.235 0.014 16.348 0.000 0.235 0.752
#> .noenergy 0.468 0.028 16.535 0.000 0.468 0.813
#> .noconcentrate 0.378 0.023 16.272 0.000 0.378 0.730
#> .appetite 0.274 0.017 16.219 0.000 0.274 0.715
#> .sleep 0.192 0.011 16.783 0.000 0.192 0.910
#> depression 1.000 1.000 1.000We can compare fit indices for our two models using the anova() function. This comparison requires that the same data be used to fit all the models of interest. So, it wouldn’t be appropriate to compare bdimod with another model fit to only 20 of the 21 BDI-II items.
Three comparison statistics are provided by anova(). With Akaike’s Information Criterion (AIC) and the Bayesian Information Criterion (BIC), we’re looking for the model with the smallest value. Smaller AIC and smaller BIC from one model to the next indicate better fit. The chi-square statistic has a p-value associated with it, where a p-value below a certain cutoff such as 0.05 would indicate significantly better fit for one model over another.
# Compare fit for BDI CFA models
anova(bdicfa2, bdicfa)
#> Chi-Squared Difference Test
#>
#> Df AIC BIC Chisq Chisq diff Df diff Pr(>Chisq)
#> bdicfa 185 19264 19464 738
#> bdicfa2 189 19310 19493 792 54.6 4 3.9e-11 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Of these three fit comparison statistics, we will focus on AIC and BIC. The AIC and BIC both increase from the model with two factors to the model with only one. This indicates poorer model fit for the depression model.
Overall, results for the unidimensional model are no better than for the previous one. The AIC and BIC are both larger, and the CFI and RMSEA are relatively unchanged. Most loadings are moderately positive, but some leave a substantial amount of item variability unexplained. For example, the item error terms (in the Std.all column of the Variances table) for sleep and noenergy are both larger than 0.80. These results indicate that more than 80% of the variability is unexplained for these items. Errors for the remaining items are all above 0.50.
Taken together, the results of these CFA suggest that the two-factor and unidimensional models may not be appropriate for the BDI-II, at least in the undergraduate population with which the data were collected.
24.2 Confirming PISA Approaches to Learning
In our final demonstration, we’ll fit a CFA to the PISA Approaches to Learning items. Our first factor structure is similar to what we explored previously via EFA. However, here, our items are only allowed to load on their intended factors. We’re hypothesizing that any cross loadings on other factors are negligible and not essential to the underlying factor structure for the instrument.
# CFA with PISA approaches to learning scale
# Specify the factor structure
almod <- lavaanify(model = "
# Three factors
memor =~ st27q01 + st27q03 + st27q05 + st27q07
elab =~ st27q04 + st27q08 + st27q10 + st27q12
cstrat =~ st27q02 + st27q06 + st27q09 + st27q11 +
st27q13",
auto.var = TRUE, auto.cov.lv.x = TRUE, std.lv = TRUE)
# Fit the model
alcfa <- cfa(almod, sample.cov = cov(pisagbr[, alitems]),
sample.nobs = 3514)
# Print output
summary(alcfa, fit = TRUE, standardized = TRUE)
#> lavaan 0.6-9 ended normally after 20 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 29
#>
#> Number of observations 3514
#>
#> Model Test User Model:
#>
#> Test statistic 1474.664
#> Degrees of freedom 62
#> P-value (Chi-square) 0.000
#>
#> Model Test Baseline Model:
#>
#> Test statistic 12390.734
#> Degrees of freedom 78
#> P-value 0.000
#>
#> User Model versus Baseline Model:
#>
#> Comparative Fit Index (CFI) 0.885
#> Tucker-Lewis Index (TLI) 0.856
#>
#> Loglikelihood and Information Criteria:
#>
#> Loglikelihood user model (H0) -52923.964
#> Loglikelihood unrestricted model (H1) -52186.632
#>
#> Akaike (AIC) 105905.928
#> Bayesian (BIC) 106084.699
#> Sample-size adjusted Bayesian (BIC) 105992.552
#>
#> Root Mean Square Error of Approximation:
#>
#> RMSEA 0.081
#> 90 Percent confidence interval - lower 0.077
#> 90 Percent confidence interval - upper 0.084
#> P-value RMSEA <= 0.05 0.000
#>
#> Standardized Root Mean Square Residual:
#>
#> SRMR 0.057
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Expected
#> Information saturated (h1) model Structured
#>
#> Latent Variables:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> memor =~
#> st27q01 0.476 0.015 32.615 0.000 0.476 0.585
#> st27q03 0.509 0.014 36.402 0.000 0.509 0.644
#> st27q05 0.541 0.016 33.380 0.000 0.541 0.597
#> st27q07 0.556 0.017 33.656 0.000 0.556 0.601
#> elab =~
#> st27q04 0.470 0.016 30.098 0.000 0.470 0.534
#> st27q08 0.577 0.015 37.460 0.000 0.577 0.644
#> st27q10 0.650 0.016 41.722 0.000 0.650 0.706
#> st27q12 0.660 0.015 43.070 0.000 0.660 0.725
#> cstrat =~
#> st27q02 0.460 0.014 31.931 0.000 0.460 0.550
#> st27q06 0.562 0.014 39.938 0.000 0.562 0.662
#> st27q09 0.547 0.014 39.525 0.000 0.547 0.657
#> st27q11 0.544 0.013 40.705 0.000 0.544 0.672
#> st27q13 0.551 0.016 34.522 0.000 0.551 0.588
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> memor ~~
#> elab 0.368 0.021 17.565 0.000 0.368 0.368
#> cstrat 0.714 0.015 46.863 0.000 0.714 0.714
#> elab ~~
#> cstrat 0.576 0.017 34.248 0.000 0.576 0.576
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|) Std.lv Std.all
#> .st27q01 0.435 0.013 34.471 0.000 0.435 0.658
#> .st27q03 0.365 0.012 31.715 0.000 0.365 0.585
#> .st27q05 0.527 0.016 33.981 0.000 0.527 0.643
#> .st27q07 0.546 0.016 33.797 0.000 0.546 0.638
#> .st27q04 0.555 0.015 37.116 0.000 0.555 0.715
#> .st27q08 0.471 0.014 33.242 0.000 0.471 0.586
#> .st27q10 0.427 0.014 29.620 0.000 0.427 0.502
#> .st27q12 0.393 0.014 28.195 0.000 0.393 0.474
#> .st27q02 0.487 0.013 37.590 0.000 0.487 0.697
#> .st27q06 0.405 0.012 34.078 0.000 0.405 0.562
#> .st27q09 0.395 0.012 34.310 0.000 0.395 0.569
#> .st27q11 0.359 0.011 33.630 0.000 0.359 0.548
#> .st27q13 0.576 0.016 36.648 0.000 0.576 0.655
#> memor 1.000 1.000 1.000
#> elab 1.000 1.000 1.000
#> cstrat 1.000 1.000 1.000Model fit is not as impressive as we would hope. The CFI is 0.71 and the RMSEA is 0.13. As with the BDI-II, loadings are moderately positive, but they leave the majority of the item variance unexplained. These results suggest that the Approaches to Learning constructs may not be strong enough or distinct enough to warrant the calculation of scale scores across the memorization, elaboration, and control items.