Introduction
This vignette demonstrates how to conduct simulation-based power analysis for discordant sibling designs. These designs estimate causal effects by comparing differences between genetically related individuals, controlling for shared background.
We simulate multivariate phenotypes using the kinsim()
function, fit regression models of interest, and calculate empirical
power across multiple design conditions.
Function Overview: kinsim()
The kinsim() function is designed to simulate data for
kinship studies. It generates paired multivariate data informed by
biometric models (ACE), supporting variable relatedness levels and
covariance structures.
Key Arguments
| Argument | Description |
|---|---|
r_all |
Vector of genetic relatedness values (e.g., 1,
0.5, 0.25, 0) |
c_all |
Vector of shared environmental correlations (e.g., 1,
1,0, 0) |
npergroup_all |
Sample sizes for each level of relatedness |
ace_list |
Matrix of ACE parameters per variable (rows = traits; columns = a, c, e) |
cov_a, cov_c, cov_e
|
Cross-variable covariance for A, C, and E components |
mu_list |
Mean values for each phenotype |
r_vector |
Optional: pairwise relatedness at the observation level |
Example Usage
Step 1: Define Simulation Grid
We define a grid of simulation conditions, varying genetic relatedness, ACE variance components, and genetic correlations.
# Libraries
library(NlsyLinks)
library(discord)
library(utils)
library(tidyverse)
library(ggplot2)
# Set random seed for reproducibility
set.seed(1492)
# Disable scientific notation for clarity
options(scipen = 999)
conditions <- expand.grid(
id = 1,
total_pairs = c(100, 250, 500, 750, 1000),
relatedness = c(1, .5),
raised_together = c(1), # 1 if raised together, 0 if apart
cov_a = c(0, 0.25),
cov_c = c(0, 0.25),
cov_e = c(0, 0.25),
ace_a = c(1),
ace_c = c(1),
ace_e = c(1)
)
conditions$id <- 1:nrow(conditions)Here, we vary the total number of sibling pairs, genetic relatedness (MZ vs. DZ), and the presence/absence of covariates influencing the phenotypes through A, C, and E pathways. The ACE variance components are held constant at 1 for simplicity. This results in a total of 80 unique conditions to evaluate.
Step 2: Run Simulations
For each condition, we simulate 100 replications of fitting
discordant sibling models. We have kept the number of trials low for
demonstration purposes, but you can and should increase
n_trials for more robust power estimates, the normal
recommendation is at least 1000 trials.
Please note that the simulations may take some time to run,
especially with larger sample sizes and more trials. Also note that the
FAST option can be set to TRUE for quicker,
less detailed analyses, or FALSE for more thorough
analyses. The FAST option drops pairs that are tied on the
outcome, because it filters only to pairs where the outcome difference
is greater than zero.
# Set number of trials (increase for more robust estimates)
n_trials <- 100
set.seed(1492) # Set seed for reproducibility
FAST <- FALSE # Set to FALSE for slower, more detailed analysis
results_list <- list()
name.results <- c("coef_xdiff", "p_xdiff", "r.squared")
for (cond in seq_along(conditions$id)) {
current <- conditions[cond, ]
temp_results <- matrix(NA, nrow = n_trials, ncol = length(name.results))
colnames(temp_results) <- name.results
for (i in 1:n_trials) {
trial <- kinsim(
r_all = current$relatedness,
c_all = current$raised_together,
npg_all = current$total_pairs,
mu_list = c(1, 1),
ace_all = c(current$ace_a, current$ace_c, current$ace_e),
cov_a = current$cov_a,
cov_c = current$cov_c,
cov_e = current$cov_e,
variables = 2
)
extract <- data.frame(
id = trial$id, r = trial$r,
y_s1 = trial$y1_1, y_s2 = trial$y1_2,
x_s1 = trial$y2_1, x_s2 = trial$y2_2
)
#
if (FAST == TRUE) {
# faster
# double enter the data and subset to ydiff > 0
extract2 <- rbind(
transform(extract,
y_s1 = y_s2, y_s2 = y_s1,
x_s1 = x_s2, x_s2 = x_s1
),
extract
)
extract2$y_diff <- extract2$y_s1 - extract2$y_s2
extract2$x_diff <- extract2$x_s1 - extract2$x_s2
extract2$x_bar <- (extract2$x_s1 + extract2$x_s2) / 2
extract2$y_bar <- (extract2$y_s1 + extract2$y_s2) / 2
# select pair with ydiff > 0
extract3 <- extract2[extract2$y_diff > 0, ]
fit <- tryCatch(
lm(y_diff ~ x_bar + y_bar + x_diff, data = extract3),
error = function(e) {
return(NULL)
}
)
}
# slower
if (FAST == FALSE) {
fit <- tryCatch(
discord_regression(
data = extract, outcome = "y", predictors = "x",
id = "id",
sex = NULL,
race = NULL,
fast = TRUE
),
error = function(e) {
return(NULL)
}
)
}
if (!is.null(fit)) {
sm <- summary(fit)
temp_results[i, "coef_xdiff"] <- coef(sm)["x_diff", "Estimate"]
temp_results[i, "p_xdiff"] <- coef(sm)["x_diff", "Pr(>|t|)"]
temp_results[i, "r.squared"] <- sm$r.squared
}
}
results_list[[cond]] <- as.data.frame(temp_results)
}Step 3: Summarize Power
Our final step is to summarize the power across all conditions. We
calculate the proportion of trials where the p-value for the difference
in means (p_xdiff) is less than 0.05, and we also report
the median R-squared value from the regression models. Note that we’ve
limited the number of trials to 100 for demonstration purposes, but you
can (and should) increase this for more robust estimates.
power_summary <- lapply(results_list, function(res) {
data.frame(
effect_detected = sum(res$p_xdiff < 0.05, na.rm = TRUE),
effect_notdetected = sum(res$p_xdiff >= 0.05, na.rm = TRUE),
total = sum(!is.na(res$p_xdiff)),
power_xdiff = mean(res$p_xdiff < 0.05, na.rm = TRUE),
median_r2 = median(res$r.squared, na.rm = TRUE)
)
})
final_results <- cbind(conditions, do.call(rbind, power_summary))Step 4: Visualize Power
We can visualize the power estimates across different conditions. The plots below show the power estimates for each condition, including the total number of pairs, relatedness level, covariate settings, and the median R-squared value from the regression models. As expected, power increases with the number of pairs and is influenced by the relatedness level and covariate settings. In the plots below, we visualize the power estimates across different conditions, focusing on the impact of covariates and relatedness levels.
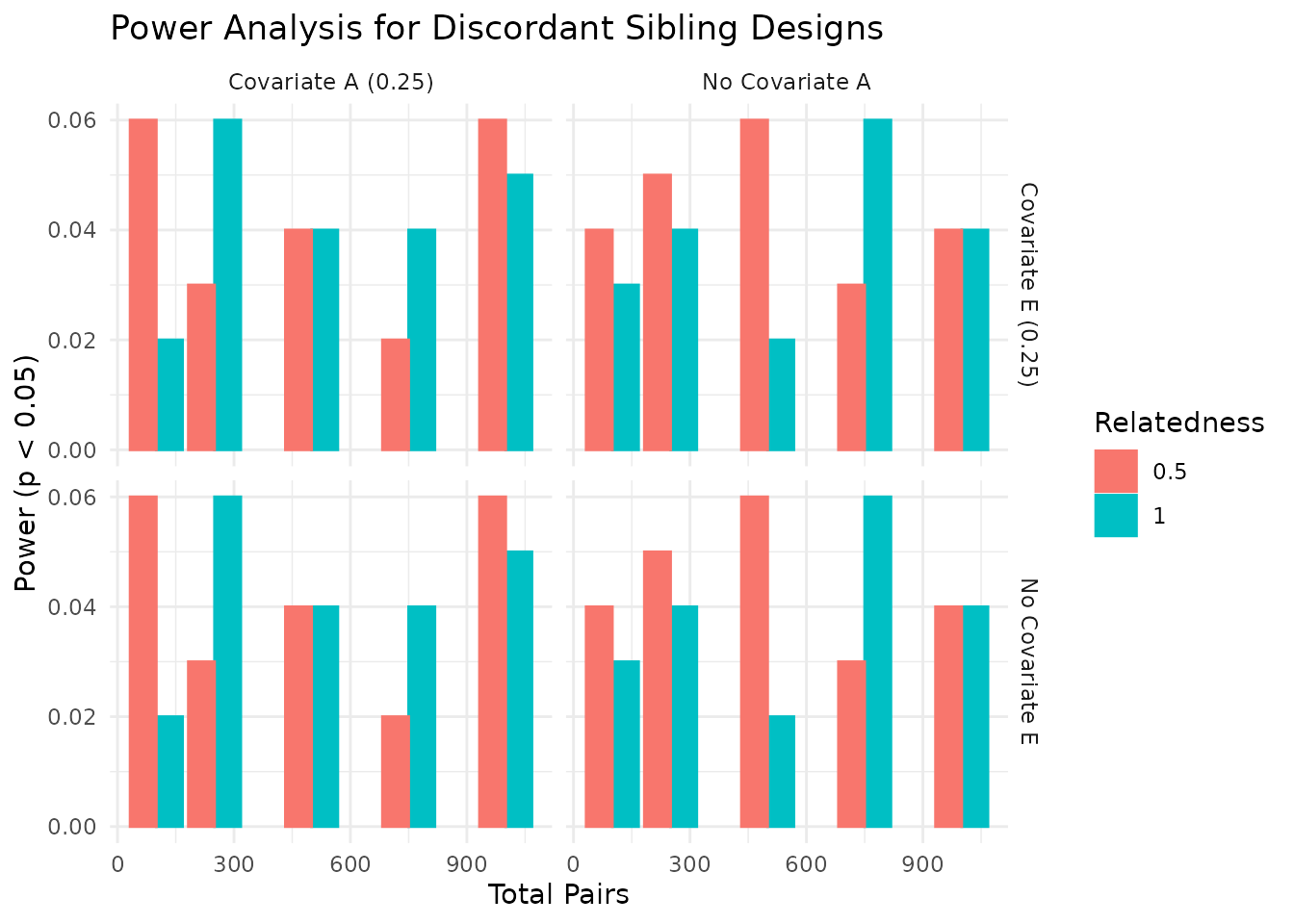
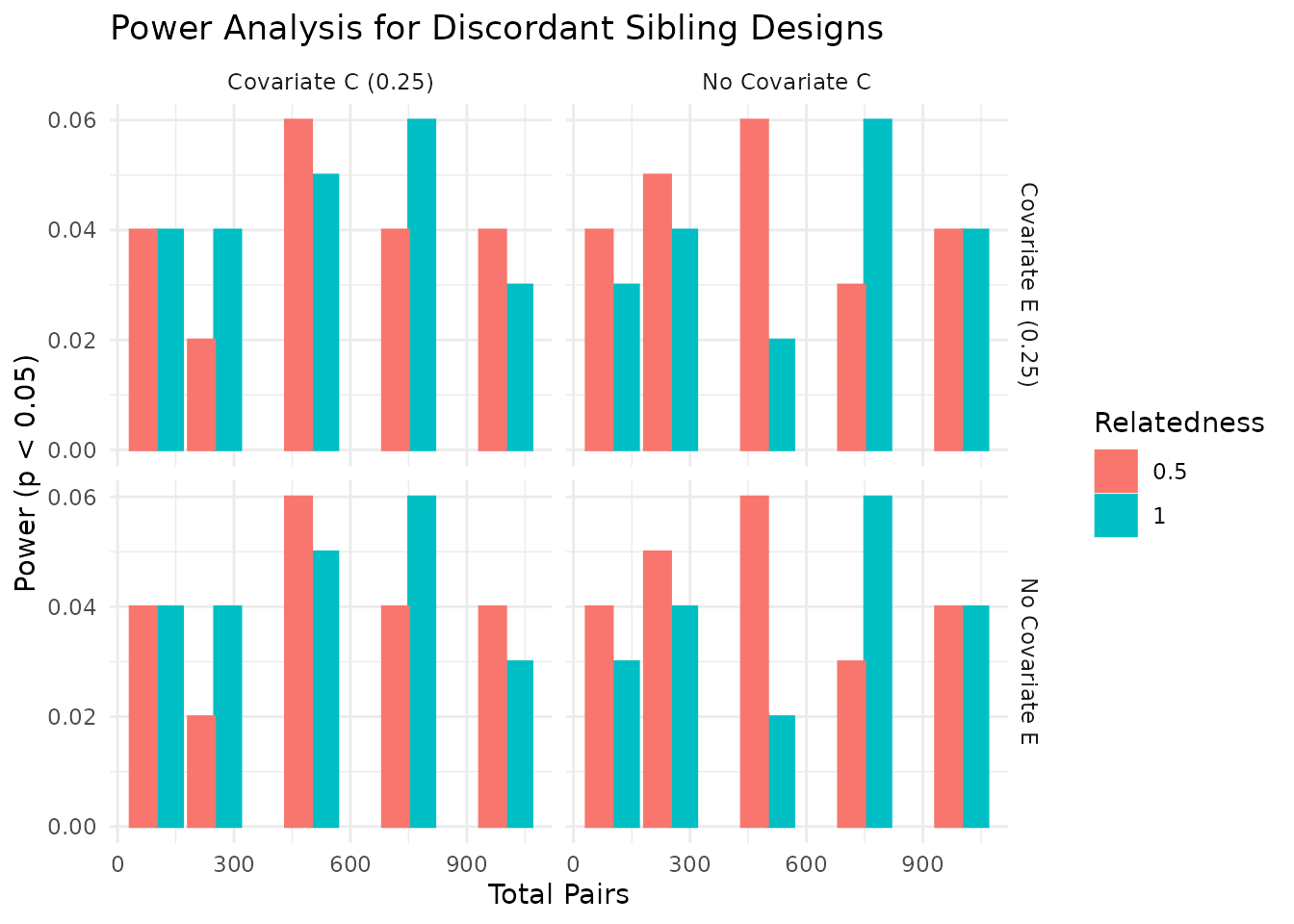
In the plots above, we see how power varies with the number of sibling pairs, relatedness levels, and the presence of covariates. The dashed lines indicate common benchmarks for power (0.80) and false positive rate (0.05). As expected, power increases with the number of pairs and is influenced by the relatedness level and covariate settings.
Power Table
The table below summarizes the power estimates across different
conditions. The power_xdiff column indicates the proportion
of trials where the p-value for the difference in means
(p_xdiff) is less than 0.05, and the median_r2
column reports the median R-squared value from the regression
models.
Conclusion
This vignette demonstrates how to conduct a simulation-based power
analysis for discordant sibling designs using the discord
package. By varying genetic relatedness, ACE variance components, and
covariate settings, we can assess the power of our designs to detect
causal effects. The results highlight the importance of sample size and
relatedness level in achieving sufficient power for these analyses.
