Network tools for finding extended pedigrees and path tracing • BGmisc

Introduction

This vignette showcases two key features that capitalize on the network structure inherent in pedigrees:

Finding extended families with any connecting relationships between members. This feature strictly uses a person’s ID, mother’s ID, and father’s ID to find out which people in a dataset are remotely related by any path, effectively finding all separable extended families in a dataset.
Using path tracing rules to quantify the amount of relatedness between all pairs of individuals in a dataset. The amount of relatedness can be characterized by additive nuclear DNA, shared mitochondrial DNA, sharing both parents, or being part of the same extended pedigree.

Loading Required Libraries and Data

library(BGmisc)
data(potter)

Finding Extended Families

Many pedigree datasets only contain information on the person, their mother, and their father, often without nuclear or extended family IDs. Recognizing which sets of people are unrelated simplifies many pedigree-related tasks. This function facilitates those tasks by finding all the extended families. People within the same extended family have at least some form of relation, however distant, while those in different extended families have no relations.

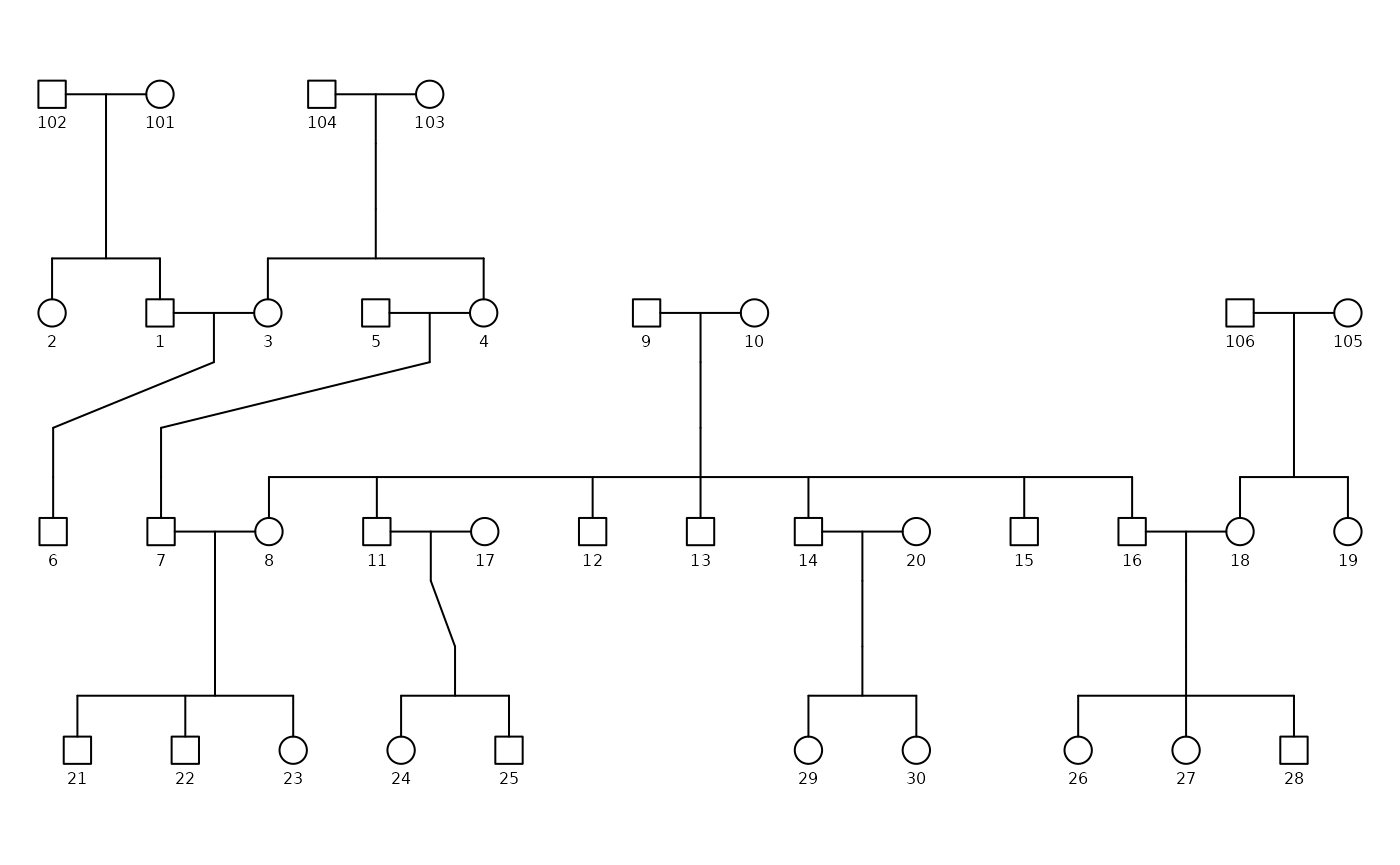
Potter Family Pedigree

We will use the potter pedigree data as an example. For convenience, we’ve renamed the family ID variable to oldfam to avoid confusion with the new family ID variable we will create.

df_potter <- potter
names(df_potter)[names(df_potter) == "famID"] <- "oldfam"

ds <- ped2fam(df_potter, famID = "famID", personID = "personID")

table(ds$famID, ds$oldfam)
#>    
#>      1
#>   1 36

Because the potter data already had a family ID variable, we compare our newly created variable to the pre-existing one. They match!

Computing Relatedness

Once you know which sets of people are related at all to one another, you’ll likely want to know how much. For additive genetic relatedness, you can use the ped2add() function.

add <- ped2add(potter)

This computes the additive genetic relatedness for everyone in the data. It returns a square, symmetric matrix that has as many rows and columns as there are IDs.

add[1:7, 1:7]
#>     1    2    3    4   5     6     7
#> 1 1.0 0.50 0.00 0.00 0.0 0.500 0.000
#> 2 0.5 1.00 0.00 0.00 0.0 0.250 0.000
#> 3 0.0 0.00 1.00 0.50 0.0 0.500 0.250
#> 4 0.0 0.00 0.50 1.00 0.0 0.250 0.500
#> 5 0.0 0.00 0.00 0.00 1.0 0.000 0.500
#> 6 0.5 0.25 0.50 0.25 0.0 1.000 0.125
#> 7 0.0 0.00 0.25 0.50 0.5 0.125 1.000

The entry in the ith row and the jth column gives the relatedness between person i and person j. For example, person 1 (Vernon Dursley) shares 0.5 of their nuclear DNA with person 6 (Dudley Dursley), shares 0.5 of their nuclear DNA with person 2 (Marjorie Dursley).

table(add)
#> add
#>      0 0.0625  0.125   0.25    0.5      1 
#>    788      6     94    208    164     36

It’s probably fine to do this on the whole dataset when your data have fewer than 10,000 people. When the data get large, however, it’s much more efficient to compute this relatedness separately for each extended family.

add_list <- lapply(
  unique(potter$famID),
  function(d) {
    tmp <- potter[potter$famID %in% d, ]
    ped2add(tmp)
  }
)

Other relatedness measures

The function works similarly for mitochondrial (ped2mit), common nuclear environment through sharing both parents (ped2cn), and common extended family environment (ped2ce).

Computing mitochondrial relatedness

Here we calculate the mitochondrial relatedness between all pairs of individuals in the potter dataset.

mit <- ped2mit(potter)
mit[1:7, 1:7]
#>   1 2 3 4 5 6 7
#> 1 1 1 0 0 0 0 0
#> 2 1 1 0 0 0 0 0
#> 3 0 0 1 1 0 1 1
#> 4 0 0 1 1 0 1 1
#> 5 0 0 0 0 1 0 0
#> 6 0 0 1 1 0 1 1
#> 7 0 0 1 1 0 1 1

table(mit)
#> mit
#>    0    1 
#> 1082  214

As you can see, some of the family members share mitochondrial DNA, such as person 2 and person 3 0, whereas person 1 and person 3 do not.

Computing relatedness through common nuclear environment

Here we calculate the relatedness between all pairs of individuals in the potter dataset through sharing both parents.

commonNuclear <- ped2cn(potter)
commonNuclear[1:7, 1:7]
#>   1 2 3 4 5 6 7
#> 1 1 1 0 0 0 0 0
#> 2 1 1 0 0 0 0 0
#> 3 0 0 1 1 0 0 0
#> 4 0 0 1 1 0 0 0
#> 5 0 0 0 0 1 0 0
#> 6 0 0 0 0 0 1 0
#> 7 0 0 0 0 0 0 1


table(commonNuclear)
#> commonNuclear
#>    0    1 
#> 1196  100

Computing relatedness through common extended family environment

Here we calculate the relatedness between all pairs of individuals in the potter dataset through sharing an extended family.

extendedFamilyEnvironment <- ped2ce(potter)
extendedFamilyEnvironment[1:7, 1:7]
#>      [,1] [,2] [,3] [,4] [,5] [,6] [,7]
#> [1,]    1    1    1    1    1    1    1
#> [2,]    1    1    1    1    1    1    1
#> [3,]    1    1    1    1    1    1    1
#> [4,]    1    1    1    1    1    1    1
#> [5,]    1    1    1    1    1    1    1
#> [6,]    1    1    1    1    1    1    1
#> [7,]    1    1    1    1    1    1    1

table(extendedFamilyEnvironment)
#> extendedFamilyEnvironment
#>    1 
#> 1296

Subsetting Pedigrees

Subsetting a pedigree allows researchers to focus on specific family lines or individuals within a larger dataset. This can be particularly useful for data validation as well as simplifying complex pedigrees for visualization. However, subsetting a pedigree can result in the underestimation of relatedness between individuals. This is because the subsetted pedigree may not contain all the individuals that connect two people together. For example if we were to remove Arthur Weasley (person 9) and Molly Prewett (person 10) from the potter dataset, we would lose the connections amongst their children.

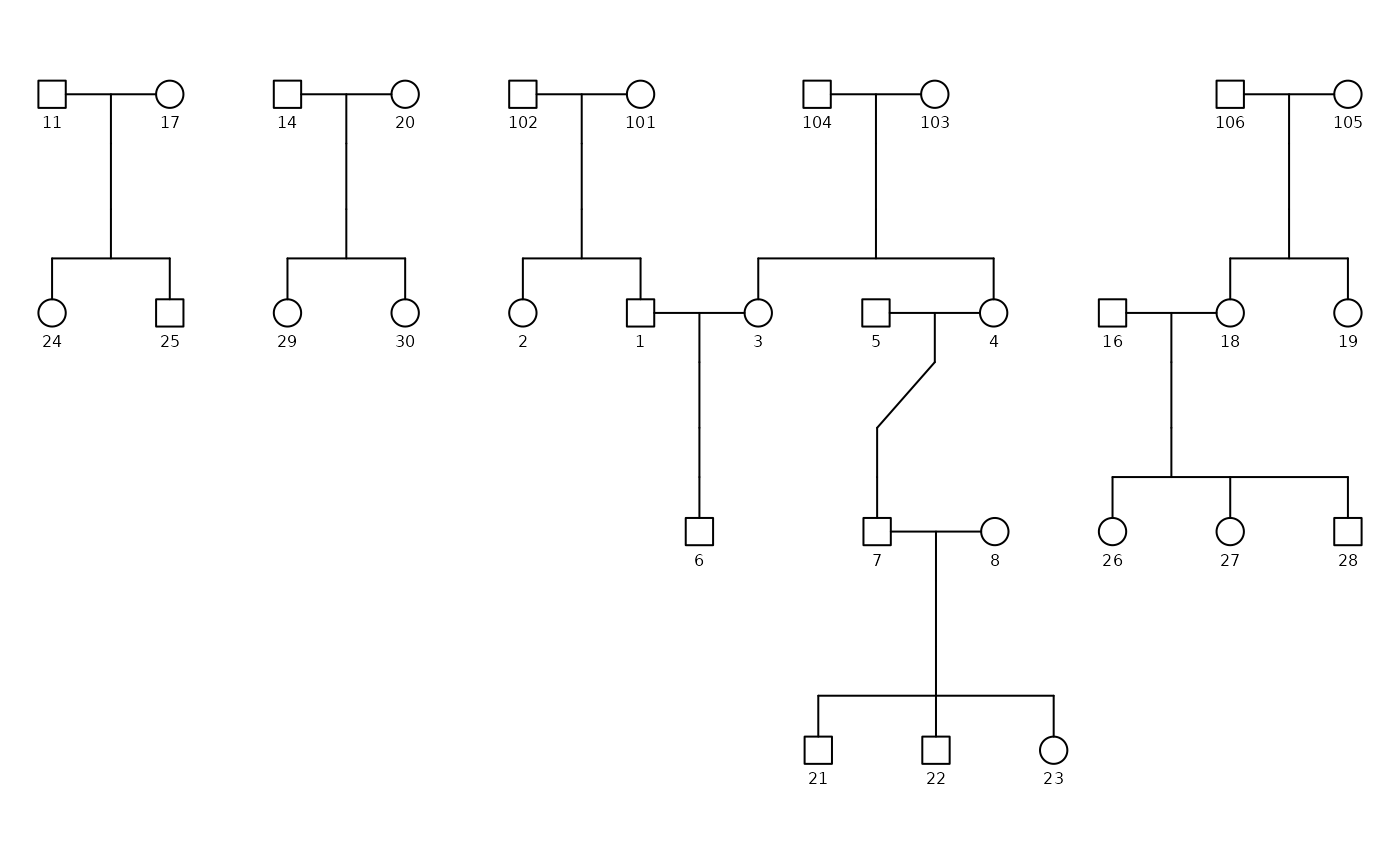
Potter Subset Pedigree

In the plot above, we have removed Arthur Weasley (person 9) and Molly Prewett (person 10) from the potter dataset. As a result, the connections between their children are lost.

Similarly, if we remove the children of Vernon Dursley (1) and Petunia Evans (3) from the potter dataset, we would lose the connections between the two individuals.

However, this subset does not plot the relationship between spouses (such as the marriage between Vernon Dursley and Petunia Evans), as there are not children to connect the two individuals together yet.

subset_rows <- c(1:5, 31:36)
subset_potter <- potter[subset_rows, ]